三角形之谜 五年（3）班  陈艺宸

                                                                三角形之谜

                                                        五年（3）班  陈艺宸

        在学完三角形知识后，爸爸出了一道题，给我留下了深刻的印象，我来给大家讲讲吧！

        题目如下：平面上有7个点，任意三点不在同一直线上，以这7个点作为顶点做三角形，使任意两个三角形至多只有一个公共点，问最多可以做出多少个满足上述条件的三角形？

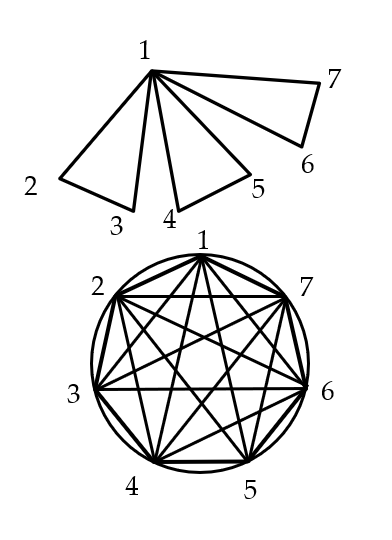
       我在纸上画了很多草图，费尽心思想得到合乎要求的7个三角形，但没有结果，只好向爸爸请教，他很快就给出了解答，非常精彩。在他的解答中有一句话使我心头一震：“在构造这7个三角形时，每一个点恰好用了3次。”事后，我又回顾了自己的思路，有两张草图印象很深，第一张是开始的草图（图一），这是第1个念头，只能做出合要求的三角形。于是，想在此图基础上连线增加符合要求的三角形，虽然有所改进，但毫无章法，很快就放弃了。

       为了改进作图，我先将7个点放在图上，可保证无三点共线，两两连线，得到以给定7个点为顶点的所有三角形（图二），我知道要求的7个三角形必在其中，但要将它们找出来，并加以说明又很困难，然而当爸爸的信息“每个点恰用三次”出现时，我的第一个念头立刻浮现在眼前，图中的“1”不正好直观地被用了3次吗？如果对1进行轮换，用2，3，4，5，6，7替换1，就可产生3×7=21个合要求的三角形，而因为每个点恰好用了3次，因此，合乎题目要求的三角形正好是7个，这7个三角形的顶点分别为（1,2,3），（3,4,5），（5,6,1），（1,7,9），（3,7,6），（5,7,2），（2,4,6），上面的想法几乎在一瞬间完成，再去复查图二，7个三角形很容易找出来了。因为其他三角形不符合要求或者重复，所以没有多余的三角形了。

       仔细回味这道题，我感觉到了数学的奇妙和魅力，更多的未解之谜正等待我们探索呢！