图形的探索 五（3） 罗鲁德

        1、问题的提出：

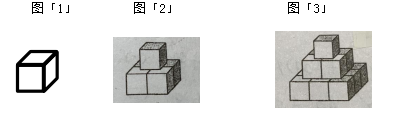
          如图:图「1」由1个棱长是1cm的小正方体堆成，图「2」由5个棱长是1cm的小正方体堆成，图「3」由14个棱长是1cm的小正方体堆成，按此规律，完成下面各题。

（1）图「10」有（ ）个小正方体；

（2）图「N」有（ ）个小正方体（n>4）。

       2、问题的解决（观察）

        通过观察我得知图「1」有1层：1；

                        图「2」有2层：1+4；

                        图「3」有3层：1+4+9.

      3、问题的解决（推论）      【备注：*表示乘】

         那么图「4」有4层：1+4+9+16=1*1+2*2+3*3+4*4

         图「5」有5层：1+4+9+16+25=1*1+2*2+3*3+4*4+5*5

                      ......

         图「10」有10层:  1+4+9+16+25+36+49+64+81+100=385

        则图「N」（n>4）就是：12+22+32+......+n2

        4、作答

      （1）图「10」有（385 ）个小正方体；

      （2）图「N」有（ 12+22+32+......+n2）个小正方体（n>4）