趣味几何问题 五年5班 吴晏如

       在这个寒假，我看到了一道很有趣的比例几何题。

       如下图，CD:BD=3:1，E是AC边上靠近A的三分点。若三角形ADE的面积为4，那么三角形ABC的面积是多少？

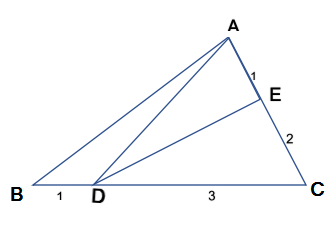
     解题思路：这道题是由一个小面积推出大面积，要按照题目给出的比例值来一步一步推。

首先，要把题目中的信息标到图上。

题目要求三角形ABC的面积，根据图形我们知道：

S△ABC=S△ABD+ S△ADC，所以只需求出三角形ABD和三角形ADC的面积就能解出此题。

       第一步：求△ADC的面积。

我们注意到△AED和△ACD是等高三角形，而且△AED的面积是4。因为E是AC边上靠近A的三分点，则AE:AC=1:3，所以S△AED:S△ACD=1:3,就可以得到：

S△ADC=3×S△AEC=3×4=12

       第二步：求△ABD的面积。

我们注意到△ABD和△ADC是等高三角形，而且，题目告诉我们BD:DC=1:3,所以：S△ABD:S△ADC=1:3，而上一步我们已经算出S△ADC=12，所以我们可以得到S△ABD=S△ADC÷3=12÷3=4

       第三步：我们已经求出S△ABD和S△ADC的面积，最后把两个三角形的面积相加，得到三角形ABC的面积：

S△ABC=S△ABD+ S△ADC=4+12=16

      总结：对于这种求三角形面积的题目，没有告诉我们边长和高，但知道其中一个图形的面积，并且有边长的比例关系，我们就需要考虑等高模型，从面积的比例着手一步一步推出答案。

     解决数学问题就要勤于思考，善于总结，看到问题背后涉及的数学思想和方法，就能够举一反三，触类旁通。